エクセルで、データの中から中央値を算出するのが『MEDIAN関数』です。
下図を用いて、MEDIAN関数の使い方を解説します。
中央値とは
データを大きい順に並べた時に真ん中にある値を指します。
値が1・2・3・4・5の場合は、中央値が3となります。
また、値が2・3・4・5の場合は、中央値が3.5となります。
MEDIAN関数の構文
次に、MEDIAN関数の構文は、次のようになっております。
=MEDIAN(数値1,数値2,~)
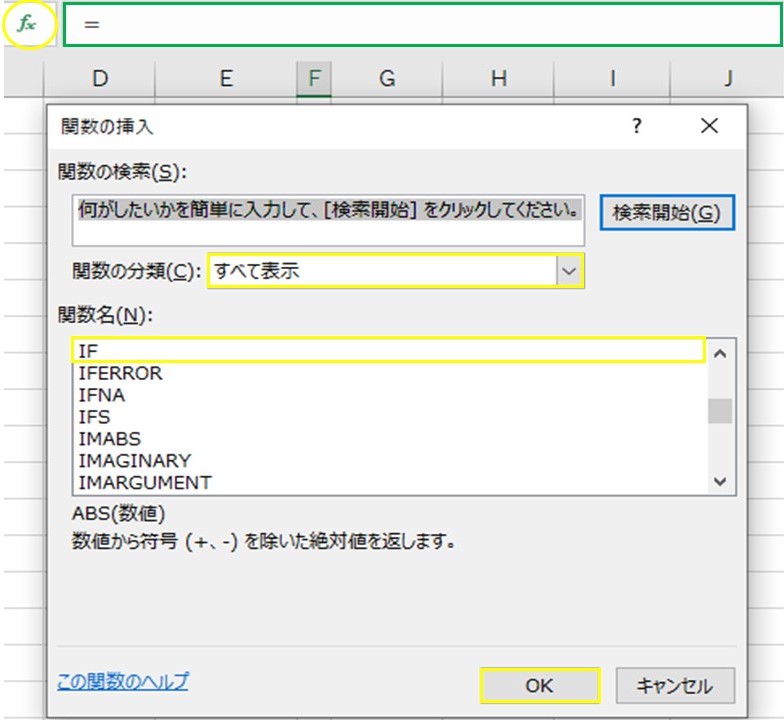
エクセル関数を使う時は、2つの使い方があります。
1つ目は、黄色の○で囲っている「fxをクリック→すべて表示を選択→該当関数を選択→OK」と入力後に、入力内容を指示した枠が表示されるので、そこに入力することです。
2つ目は、緑色の枠に構文を直接入力となります。
MEDIAN関数の使い方
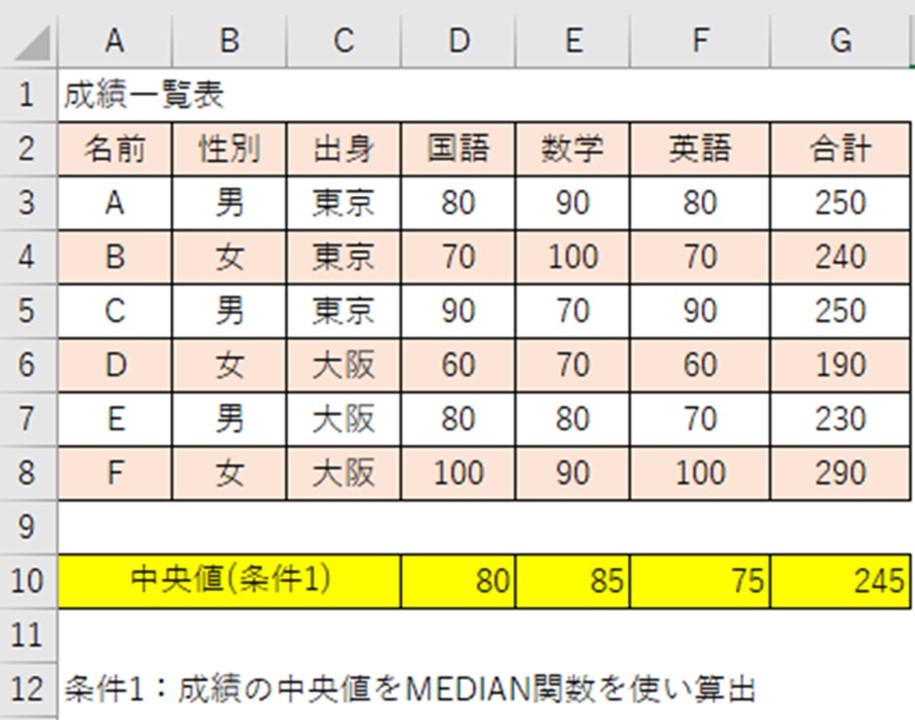
次に、「条件1:成績の中央値をMEDIAN関数を使い算出」の時の構文です。
D10セルに入力する時の関数は下記になります。
=MEDIAN(D3:D8)
数値1:中央値を算出する範囲
国語について、点数順に並び変えると、「60,70,80,80,90,100」となります。
3番目の点数が80で、4番目の点数が80で、3番目と4番目の点数を合算して2で割ると80となりますので、中央値は80
数学について、点数順に並び変えると、「70,70,80,90,90,100」となります。
3番目の点数が80で、4番目の点数が90で、3番目と4番目の点数を合算して2で割ると85となりますので、中央値は85
英語について、点数順に並び変えると、「60,70,70,80,90,100」となります。
3番目の点数が70で、4番目の点数が80で、3番目と4番目の点数を合算して2で割ると75となりますので、中央値は75
合計点について、点数順に並び変えると、「190,230,240,250,250,290」となります。
3番目の点数が240で、4番目の点数が250で、3番目と4番目の点数を合算して2で割ると245となりますので、中央値は245
中央値を計算する場合はMEDIAN関数を使う
膨大なデータから中央値を計算となると、苦戦することは必須です。
数字を並び替えて「真ん中の数字」または「真ん中の数字の前後」が分かれば、電卓を用いて計算することもできますが、数が多いほど並び替えの手間が掛かります。
その点、MEDIAN関数を使えば、すぐに算出することが出来ます。
使い方もすぐに分かる内容となっていますので、もし、中央値の計算をしなければならなくなった時は、MEDIAN関数を使って対処してください。