エクセルで、ローンの定期支払額を算出するのが『PMT関数』です。
下図を用いて、PMT関数の使い方を解説します。

ローンの返済方法の種類
ローンの返済方法には、「元利均等返済」と「元金均等返済」の2種類があります。
元利均等返済とは、毎月の返済額が一定になる返済方法を指します。
返済額は一定になりますが、元金部分の返済スピードが遅いため、元金均等返済と比較すると、返済総額が多くなります。
元金均等返済とは、毎月の元金の返済額が一定になる返済方法を指します。
元利均等返済と比較すると、前半の返済額は大きいですが、後半になるにつれて返済額が小さくなり、返済総額は少なくなります。
PMT関数の構文
次に、PMT関数の構文は、次のようになっております。
=PMT(利率,期間,現在価値,将来価値,支払期日)
エクセル関数を使う時は、2つの使い方があります。
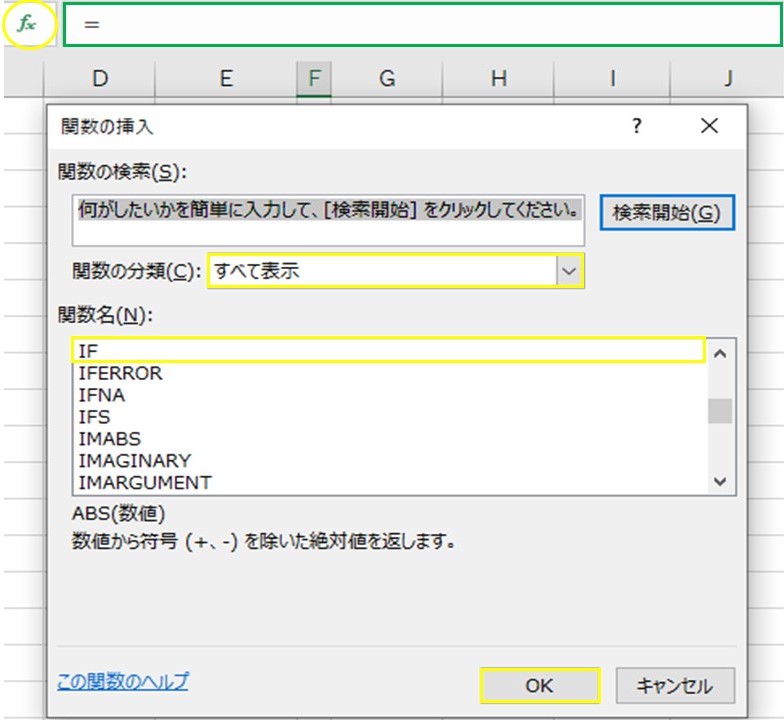
1つ目は、黄色の○で囲っている「fxをクリック→すべて表示を選択→該当関数を選択→OK」と入力後に、入力内容を指示した枠が表示されるので、そこに入力することです。
2つ目は、緑色の枠に構文を直接入力となります。
PMT関数の使い方
次に、「条件1:ローンの定期支払額をPMT関数を使い算出」の時の構文です。
H3セルに入力する時の関数は下記になります。
=PMT(B3,C3,D3,E3,F3)
利率:期間あたりの利率(年単位ならば年利率、月単位ならば月利率)
期間:返済期間
現在価値:返済前の金額
将来価値:返済後の金額
支払期日:支払いがいつ行われるか(期首ならば1、期末ならば0)
※PMT関数は、手元に入る金額が「+」表記、手元から出る金額が「-」表記で記載されるため、返済額がマイナス表記されています。
プラス表記にしたい場合は、関数の設定時に、「=PMT」を「=-PMT」とします。
例題は、元利均等返済時の毎月の返済額の算出となります。
240,000円の借入金額を、年利0%で、2年後に、返済する場合の毎月の返済額は、10,000円
240,000円の借入金額を、年利3%で、2年後に、返済する場合の毎月の返済額は、10,315円
240,000円の借入金額を、年利5%で、2年後に、返済する場合の毎月の返済額は、10,529円
元利均等返済の計算式
毎月の返済額の算出数式は下記の通りです。
毎月の返済額={借入金額×月利×(1+月利)^返済回数}÷{-1+(1+月利)^返済回数}・・・(^は累乗)
この数式を、先程の例題に照らし合わせると
240,000円の借入金額を、年利0%で、2年後に、返済する場合の毎月の返済額は、年利が0%のため、利率を考慮する必要がありませんので、240,000円÷24ヶ月=10,000円
240,000円の借入金額を、年利3%で、2年後に、返済する場合の毎月の返済額は、{240,000円×(3%÷12ヶ月)×(1+(3%÷12ヶ月)^24}÷{-1+(1+(3%÷12ヶ月)^24}=10,315円
240,000円の借入金額を、年利5%で、2年後に、返済する場合の毎月の返済額は、{240,000円×(5%÷12ヶ月)×(1+(5%÷12ヶ月)^24}÷{-1+(1+(5%÷12ヶ月)^24}=10,529円
となり、PMT関数で設定を正しく行うと、自動計算が出来ることが分かります。
元利均等返済の定期支払額の算出時はPMT関数を使う
元利均等返済での毎月の支払額は、住宅購入を検討している人は、支払方法を検討する時に、目にする機会があると思います。
実際の返済額は、業者の見積もりを取らないと、明らかになりませんが、返済額のシミュレーションをしたい時は、有効な関数となります。
毎月の返済額の目星を付けたい時は、PMT関数を使ってみましょう。